What are Option Greeks?

Options traders often use the “Greeks” to measure the sensitivity of an option’s price to its underlying determining parameters, such as volatility or the price of the underlying asset. The Greeks can also measure a particular option or portfolio.
Delta, Gamma, Vega, Theta, and Rho are the key option Greeks, and these variables are called Greeks because they are typically associated with Greek symbols.
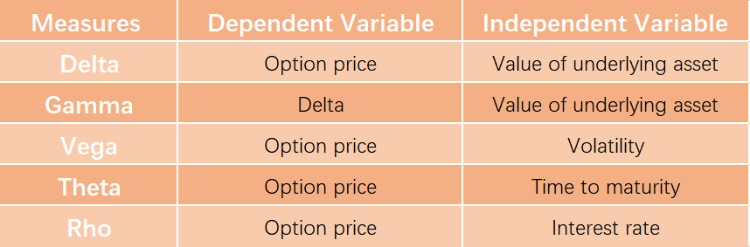
Note: Dependent variable means something that depends on other factors, while independent variable stands alone and isn't changed by the other variables.
Each risk variable above is a result of an imperfect assumption or relationship of the option with another underlying variable. It’s important to remember that the Greeks are based on mathematical formulas. Given these complicated formulas used to determine the Greeks and the importance of accurate results, they are most often calculated using a computerized solution. Traders use different Greek values to assess options risk, and Investors use them both to make new investment decisions and to analyze the risk of their current portfolio.
Option Greek: Delta
Delta gauges the rate of change between the option's price and a $1 change in the underlying asset's price. In other words, the price sensitivity of the option relative to the underlying. The delta is usually calculated as a decimal number from -1 to 1.
For call options, Delta has a range from 0 to 1 while the delta of put options has a range from -1 to 0. For example, assume an investor is buying a call option with a delta of 0.50, so if the underlying stock increases by $1, the option's price would theoretically increase by 50 cents.
Delta is also known as a hedge ratio. If a trader knows the delta of the option, he/she can hedge his/her position by buying or shorting the number of underlying assets multiplied by delta. For example, if you purchase a standard American call option with a 0.50 delta, you need to sell 50 shares of stock to be fully hedged.
Delta is also used when determining directional risk. To simply put, positive delta means traders adopt a positive (call/buy) approach to the market, whereas negative deltas are triggers for negative (put/sell) assumptions.
Option Greek: Gamma
An option’s gamma measures the rate of change in delta relative to the changes in the price of the underlying asset over time. If the price of the underlying asset increases by $1, the option’s delta will change by the gamma amount. Since delta values are constantly changing with the underlying asset's price, gamma is used to measure the rate of change and provide traders with an idea of what to expect in the future. This makes gamma useful for determining the stability of delta, which can be used to determine the likelihood of an option reaching the strike price at expiration. Gamma will be a number anywhere from 0 to 1.
Generally, call options have a positive gamma. An option has a maximum gamma when it is at-the-money (option strike price equals the price of the underlying asset). However, gamma decreases when an option is deep-in-the-money or out-of-the-money.
Gamma would be highest for options that are at-the-money and closer to expiration. The higher Gamma is, the more unstable Delta is as the price of the underlying stock changes. Therefore, high gamma values mean that the option tends to experience volatile swings, which is a bad thing for most traders looking for predictable opportunities.
Option Greek: Vega
Vega measures the sensitivity of an option price relative to the volatility of the underlying asset. If the volatility of the underlying assets increases by 1%, the option price will change by the vega amount. While delta measures actual price changes, vega is focused on changes in expectations for future volatility, which tells us approximately how much an option price will increase or decrease given an increase or decrease in the level of implied volatility.
For example, with AAPL trading at $150, the Nov 150 call has a price of $9 and a Vega of 0.25. If volatility expands by 1% and all else remains the same, the price of the Nov 150 call should increase by 0.25 to $9.25.
One should note that when option prices are bid up, it implies volatility will increase because there are more buyers. Meanwhile, long positions benefit from volatility expansion because their Vega is positive. Short positions benefit from volatility contraction because their Vega is negative.
Option Greek: Theta
Theta measures the sensitivity of the option price relative to the option’s time to maturity. It represents if the option’s time to maturity decreases by one day, the option’s price will change by the theta amount. The Theta option Greek is also referred to as time decay, which means the erosion of an option's value or price due to the passage of time. As time passes, the chance of an option being profitable or in-the-money lessens. Time decay tends to accelerate as the expiration date of an option draws closer because there's less time left to earn a profit from the trade.
For example, with AAPL trading at $150, the Nov 150 call has a price of $9 and a Theta of -0.08. That means that if one day passes and all other factors remain the same, the price of the Nov 150 call should drop to $8.92.
In most cases, theta is negative for a single option since time moves in the same direction. As soon as an option is purchased by a trader, the value of the option immediately begins to diminish until it expires and becomes worthless at the predefined expiration date. However, time decay is good for the seller of an option because as time passes, the chances increase of the option expiring with no action taken.
Option Greek: Rho
Rho measures the sensitivity of the option or options portfolio relative to interest rates. For example, if an option or options portfolio has a rho of 1, then for every 1 percentage-point increase in interest rates, the value of the option (or portfolio) increases by 1%.
Options that are most sensitive to changes in interest rates are those that are at-the-money and with the longest time to expiration. Also, Rho is larger for options that are in-the-money and decreases steadily as the option changes to become out-of-the-money. However, the rho is considered the least significant among other option Greeks because option prices are generally less sensitive to interest rate changes than to changes in other parameters.
Summary:
- An option's "Greeks" describe its various risk parameters. There are five primary Greek risk measures known as an option's Delta, Gamma, Vega, Theta and Rho.
- Delta gauges the rate of change between the option's price and a $1 change in the underlying asset's price. In other words, the price sensitivity of the option relative to the underlying.
- An option’s gamma measures the rate of change in delta relative to the changes in the price of the underlying asset over time. If the price of the underlying asset increases by $1, the option’s delta will change by the gamma amount.
- Vega measures the sensitivity of an option price relative to the volatility of the underlying asset. If the volatility of the underlying assets increases by 1%, the option price will change by the vega amount.
- Theta measures the sensitivity of the option price relative to the option’s time to maturity. It represents if the option’s time to maturity decreases by one day, the option’s price will change by the theta amount.
- Rho measures the sensitivity of the option or options portfolio relative to interest rates. The rho is considered the least significant among other option Greeks because option prices are generally less sensitive to interest rate changes than to changes in other parameters.



